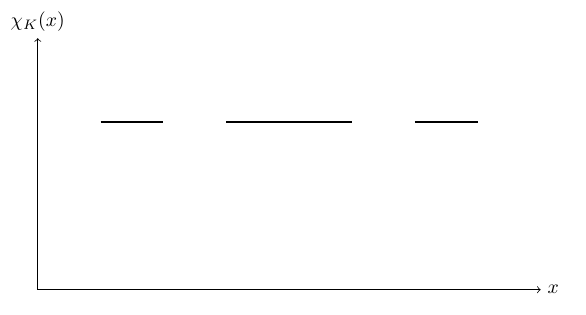泛函分析

2023年11月09日 1.3k 字大概 5 分钟

Functional Analysis

占坑，泛函分析复习笔记，内容大概有：

到2.2章节除了1.5章所有作业题解答以及部分未布置的题；
- faMidNotes.pdf 部分笔记，剩余习题有的不在范围内，选择性重做一遍。
部分定理手动证明；
往届期中真题自己的解答；（不正式写了）

Ciarlet 相关有趣的内容整理（期中前）

易混淆的点：

是指的所有线性包（即有限线性组合）的并；
基要满足两点：
- 向量族的元线性无关，即对于任意有限子集各元素线性无关；
- 对于任何，都存在有限子族，被子族里面的向量线性表示。
- 注意：任意向量空间均存在基（引理），且基的基数唯一确定。

补充例子与结论

强调（1.3里面常用结论）

中任意有界集为列紧集；

列紧空间的任意（闭）子集都是（自）列紧集；

列紧空间必是完备空间；

完全有界的度量空间可分。

定理任何有限维空间均是可分的。

要证明这个定理，首先有：有限维空间的范数相互等价，于是换一个范数证明可分。

设为的一组基，对于扩充的实数，定义映射：

则有为上的范数，且空间是可分的，取坐标为有理数的点即可。

定理设为可分的空间，则存在的有限维子空间的可数有限族满足：

证明由稠密性，设，满足

首先可以假设对任何。此时递推地定义向量族为：

那么，满足所有条件。

定理任意向量空间均可赋范。

证明取的基，对任意给定向量，唯一地存在有限子族，被子族里面的向量线性表示。
此即，那么下面映射就是上的一个范数:

定理赋范空间，可有内积给出满足平行四边形法则。并且满足平行四边形法则时，是内积。

定理是可分的。时不可分。

证明不妨证的情况，时构造稠密子集如下：
$$
A:=\bigcup\limits_{n=1}^\infty{(y_i){i=1}^\infty\in\mathcal{l}^p;y_i\in\mathbb{Q}\ when \ i\leq n,y_i=0\ elsewhere}.
$$
时，考虑为中所有以组成的数列集合，则$\forall x,y\in B,\Vert x-y\Vert\infty=1 $，且$ B $是不可列的。设$ C $是$ \mathcal{l}^\infty $中任意稠密子集，任给$ x\in B $，存在$ y(x)\in C \ s.t.\Vert x-y(x)\Vert_\infty<\frac{1}{2} $，故映射$ x\to y(x) $为单射，$ C $不可列，从而$ \mathcal{l}^\infty$不可分。

定理为中的开子集，上紧支集连续函数在中稠密。是可分空间，时不可分。

在中稠密，时不稠密。

强调（有限维的情况）

任意两个范数等价；

任何有限维赋范空间可分；

对于有限维赋范空间中的子集，紧等价于有界闭；

空间的有限维子空间在中闭；

空间是有限维的等价于的单位球面列紧。

证明第三条：对于，由于紧蕴含有界闭只需反过来证明自列紧。取的基，有界推得各个系数有界，故找到了收敛的子列，这证明了自列紧。

定理为任意向量空间，则在上存在不等价的范数。

证明取的基，那么下面映射就是上的范数:

这时取一个中的可数子族，不妨设为，令，得到。

定理为赋范空间且是有限维的，则由到的任何线性算子均是连续的。

证明选取基展开，证明。

定理（投影映射相关）

是内积空间中的非空闭凸子集。为投影映射，代表的是关于的最佳逼近元。

为连续映射，常数为1。
为线性的充要条件是是的子空间，此时的算子范数为1。

定理（正交补相关）

是内积空间中的非空子集。

是的闭子空间；
；
如果是闭的，。

定理（空间中的表示定理）

为上的空间，对任意给定的，存在唯一的向量，使得而且。

例子（空间中不是闭的子空间）

在希尔伯特空间中构造一个不是闭集的子空间的经典例子是考虑无限维空间中的有限维子空间。

以序列空间为例，这是所有平方可和的复数序列构成的空间。一个元素满足。在这个空间中，我们可以考虑子空间由所有最终变为零的序列构成，也就是说，对于中的每个序列，存在一个整数使得所有的。

尽管是的一个线性子空间，它不是闭的。这是因为可以构造一个序列的序列（也就是一个序列的极限），这个极限在中，但不在中。例如，考虑序列其中是一个序列，它的前个元素是，之后的元素都是零。每个都在中，但它们的极限是序列，这个极限在中但不在中，因为没有一个点使得序列之后的所有元素都是零。

因此，是中的一个不闭子空间的例子。

Ciarlet 相关有趣的内容整理（期中后）

未完待续…

随便寄1

2023年10月15日 8 字大概 1 分钟

这是一篇加密文章，需要密码才能阅读。

实分析练习题

2023年06月30日 2k 字大概 7 分钟

实分析补充练习与补充知识点

6.30

设定义在上的函数满足。若且，证明。

不妨设为有界集，因为对每个，可令，这样就有，再由即得结论。

对于有界零测集，设。任给，存在开集，且。对使用开集结构定理，任意构成区间满足，故，这便证明了。

设是上的连续函数，是上的实值可测函数，则是上的可测函数。

上可测函数列满足，且依测度收敛到0，证明。

是上的正值可积函数，是一列可测子集，且有，证明。

设存在一列，那么足够大时。选取的子列使得在第项上的积分值小于。简便起见，这个子列仍记为。定义，作为Fatou-Lebesgue定理的直接推论，其测度。我们有：

这推出在上几乎处处为零，与题设矛盾。

7.1

补充上面的定理证明：

补充1 Fatou-Lebesgue定理

对于给定的度量空间，假设是一系列定义在其上的实值可测函数。如果存在一个勒贝格可积函数在上以绝对值控制该序列，即对于所有自然数，都满足，那么：

证明：所有的以及的下限和上限序列在绝对值上被控制，因此它们是可测的，并且是可积的。第一个不等式是通过将非负函数应用于Fatou引理，并利用Lebesgue积分的线性性得到的。最后一个不等式是反向Fatou引理。这里的Fatou引理比我们学的要强一些（周民强4.2例题4），我们学的是非负函数列+几乎处处收敛，这里的条件是，其形式是：

总的来说，就是Fatou引理加上的控制，就能得到Fatou-Lebesgue定理！

补充2 各种收敛性

考试可能涉及到各种收敛性，这里做出一定总结：

几乎处处收敛

引理1 若，那么对任意，有

证明：的上极限集合必然不是收敛点，那么，再由递降集合测度的极限性质，得到：

Egorov定理 为几乎处处有限，定义在有限测度集合上的可测函数列。若，则对，存在，使得在上一致收敛于。

证明我看过一遍了，要用到上面的引理。取定之后，先把分解为，每一个对应使得

从而构造

进一步说明在上一致收敛于。

注意

条件不可去掉，否则考虑上的特征函数。
在下，近一致收敛于几乎处处收敛等价，二者都能推出依测度收敛。

依概率收敛

定理为几乎处处有限，定义在有限测度集合上的可测函数列。若，且几乎处处有限，则依测度收敛于。

由上述引理1立即得证。

Riesz定理 依测度收敛序列存在几乎处处收敛子列。

补充3 Lusin定理

Lusin定理描述了可测函数和连续函数的关系。其叙述如下：

是定义在的几乎处处有限可测函数，任给，存在闭集使得是上的连续函数。

首先我们需要知道，对于可测函数，存在简单紧支函数列使得并且逐点收敛。特别地若有界，该收敛是一致的。利用这一点重要性质，从简单函数出发可得Lusin定理。Lusin定理有若干推论：

推论1 是定义在的几乎处处有限可测函数，任给，存在上的连续函数满足：

若，上述的可取为紧支的。

推论2 是定义在的几乎处处有限可测函数，则存在上的连续函数列满足：

7.2

设，证明。

证明：等价于证明级数在上几乎处处收敛即可。我们用积分说明该级数在上几乎有限：

第一步是因为为非负可测函数列，可以逐项积分。上面的式子说明在上几乎处处有限，故在时上几乎处处收敛于0。

补充4 基本换元

对，，有：

证明思路：先证明对简单函数成立，再用简单函数逼近可测函数。

补充5 控制收敛定理相关

首先，DCT证明了更强的收敛。简单的记忆就是：控制函数+几乎处处收敛，极限符号可以挪到里面去。DCT有一些应用，为了强化理解，下面列举并证明两个有用的推论：

推论1（逐项积分）

不同于非负可测函数列的逐项积分定理，这里的表述是：

设，若有，那么函数项级数在上几乎处处收敛，且且

证明：为非负可测函数列，故可以逐项积分。即：

从而且几乎处处有限。命，则。而在上几乎处处有即被可积函数控制。由DCT立得：

推论2（积分号下求导）

是定义在上的函数，作为的函数在上可积，作为的函数在上可微。若存在使得：

那么有如下成立：

证明：当足够小的时候，由微分中值定理有：

再利用DCT，得到：

补充6 可积函数与连续函数的关系

上的可积函数可以被紧支连续函数逼近。任给，存在紧支连续函数和函数满足且。换言之，存在上的紧支连续函数列地并且几乎处处收敛于。
平均连续性：。
上的可积函数可以被紧支阶梯函数逼近，即存在上的紧支阶梯函数列地并且几乎处处收敛于。

补充7 重积分与累次积分

Fubini定理和Tonelli定理部分在周民强上已经过了一遍了，就不在这里写了

7.3

补充8 不定积分的微分

引理2 设，令，（当时），那么有：

证明思路：表达式写开，用Tonelli定理再加上平均连续性即得。

Lebesgue微分定理（一维版本） 设，令，则。

证明：

step1，几乎处处可微，这是因为为两个单增函数的差，故几乎处处可微。

step2，因为几乎处处可微，对于，可假设其几乎处处收敛到上的可测函数上，又由引理2，在意义下收敛于，故只需要证明。

step3，证明（不等式即Fatou引理）：

定理对于也是成立的，将定理应用在上的可测集上立刻得到上几乎处处的点都是Lebesgue密度点。下面证明一个有用的推论：

推论若在上局部可积，则几乎每个点属于的Lebesgue集。

证明：将Lebesgue微分定理应用于函数，则对于每个有理数，存在测度为零的集合，只要就有：

记，则，且对所有，存在使得。我们有：

补充9 绝对连续函数

，，则，且。

定义对于定义在上的实值函数，若对任意，存在使得只要且区间内部不交就有

则称绝对连续(AC)。绝对连续函数具有以下性质：

AC函数是一致连续且有界变差的；
如果，在上几乎处处可微，并且是上的可积函数。
微积分基本定理成立；
如果，那么对于任意中的零测集，；
如果，为中的可测集，那么可测；
若满足以下条件，。
- 如果，则；
- ；
- 。

绝对连续函数有着强于有界变差函数的结论：

定理如果，则几乎处处存在。此外，若几乎处处为零，则为常数。

暂时更新到这里，剩下的时间要回顾stein上的习题，再就泡在周民强里面了。晚上争取把chap2的习题全都过一遍。

实分析想法寄录

2023年06月11日 2.3k 字大概 9 分钟

考虑下面的问题：

给定区间上的一个具有正测度的类集合，的补集记为。对于上的特征函数，考虑在上点处的导数，这是否为0？

这一点由于微分定理是显然的，因为测度为正，故在上地有。但是换一个角度来看，这一点或许还没有那么直观。

选定一个，考察小区间，这个区间内部取0或1，如果，那么随着，中取1的部分的（测度）占比趋于零。而在缩小的取值之时，无论怎么缩小，中总是会包含无数个取值为1的闭区间，又怎么证明这些闭区间的测度之和与的比值趋于0呢？这是一个很复杂的问题，因为在附近的行为很怪异。加上类集合的选取本身就多种多样，如果没有微分定理，单纯用极限理论来看待处的微分的话，确实复杂。这也让我体会到了微分定理的深刻性，对于这样棘手的问题会有如此优雅的结论。当时我转念一想，对于集$C^ $和$ x\in C^ $，$ f(x) $在$ x $处均不可微，而$ C^ $零测，从而$ f $在$ C^ $仍是$ \mathrm{a.e.} $地为的，导不出矛盾。这就引发了我对$ \mathrm{Lebesgue}$微分定理深究的兴趣，藉此机会我们从可积函数出发，梳理一下勒贝格积分与微分理论。

积分理论

积分的定义

引理对于支撑在有限测度集合上的有界函数（BF），为任何以为界的简单函数序列，且对有，那么有

存在；
若，那么。

这样，定义BF函数的积分为。

而对于非负函数，去掉BF的条件后，其积分定义为，其中。

对于一般的函数，其积分定义为。当是我们说可积。

定理（有界收敛定理） 为一串以为界，支撑在有限测度集合的可测函数序列，且，则可测、有界、支撑在上，且

总结来说就是有界BF函数+几乎处处收敛推得可积+积分值收敛。

定理（法图引理） 为一串非负的可测函数，且，则

这是一个很反直觉的结果，这个结论的证明也相当巧妙。简言之就是选取了，而构造了，这样不仅有，还始终有，这样就得证了。直觉似乎告诉我们几乎处处收敛于，积分也会足够靠近，然而我们最终得到的却是这样一个不等式。trick或许在于的定义。如果是BF函数一切等号都能取到，然而不是BF函数的时候，根据上面的定义才诞生了这个不等式。

推论是一个非负可测函数，为一串满足的函数列，且，则

相应地单调收敛定理是更弱的推论。一个有用的推论是，无穷非负可测函数项级数的积分可以逐项积分。

可积函数的重要性质

对，存在有限测度集使得

**（绝对连续性）**存在使得只要，就有

第一个结论，令，其中是以原点位中心半径为的球。由单调收敛定理即证。第二个结论，我们思路差不多，但是构造的是截断函数，由单调收敛定理仍有。后面将写为，前者由收敛性控制，后者由截断函数的上界控制。

控制收敛定理 为可测函数序列，且，，其中可积，那么

微分理论

为了证明勒贝格微分定理，我们先引入哈代-李特尔伍德极大函数。

定义（哈代-李特尔伍德极大函数） 对于上的可积函数，定义其极大函数：

极大函数具有以下性质：

可测；
几乎处处有限；
（弱型不等式）对所有，满足：

此外还有性质如：

对有。
若对于上的可积函数，不几乎处处为0，那么对某个和所有，有$f^(x)\geq c/|x|^d $，从而有$ f^(x)$不可积。

(3)的形式比切比雪夫不等式弱。切比雪夫不等式说的是，对于非负可测函数：

这个不等式放缩其实很松。将挪过去，等号左边代表的是高为，宽为大于的部分，这一部分面积显然被包围。(1)很好证明，只需注意到集合是开集；而(2)是(3)的直接推论，下面着手证明(3)。在证明之前还需要证明重要的：

覆盖引理 设是中的有限开球簇，则存在的不相交子集使得

定理的证明是构造性的。我们先选出最大的球，将半径扩大为原有3倍之后变为，所有的与相交的球都会被完全涵盖在之内。去掉这些被完全包含的球，重复这种操作即构造成立。下面证明弱型不等式。

(3)的证明：

要证明。对于每一个，都存在对应的球使得，此即

取定的一个紧子集，选取的有限子覆盖并且选取其覆盖。则有如下不等式成立：

命题得到了证明。下面着手证明勒贝格微分定理。

微分定理 若在上可积，那么对有：

仅需证明对每个，集合

测度为0。由于紧支撑连续函数在中稠密，对于任何，存在紧支撑连续函数使得。对与连续函数，式显然成立。我们可以将写为：

两边同时取上极限并且利用三角不等式得到：

再定义：

则由切比雪夫不等式和弱型估计得到：

显然有包含关系，选取与足够靠近的即证。

remark：对于局部可积函数，上述结论仍然成立。

其他定义及结论：

定义（勒贝格密度点） 是可测集，，定义为的勒贝格密度点，若：

则几乎每个是的勒贝格密度点；几乎每个不是的勒贝格密度点。

定义（勒贝格集） 在上局部可积，则的勒贝格集由所有满足：

的组成。并且的连续点属于勒贝格集。并且有定理：若在上局部可积，则几乎每个点属于勒贝格集。

实分析chap2,3其他结论

可积函数空间

定理向量空间在它的度量下是完备的。

推论柯西列存在几乎处处收敛子列。

定理以下函数簇在中稠密：

简单函数（有限测度可测集的特征函数的有限线性组合）
阶梯函数（cube的特征函数的有限线性组合）
紧支撑连续函数

平移不变性 为可积函数，定义。则

这是紧支撑连续函数在中稠密的推论。

定理

假定在上可积，则：

截面在上可积；
在上可积；

此外，还满足等式：

作为一个应用，有如下的结论：

定理假定在上非负可测，则对，有：

截面在上可测；
在上可测；
在扩充的意义下，满足等式：

上的可测子集，将定理应用到上，得到如下的：

推论对，是上的可测子集，且：

关于集合的可测性的若干命题

为上的可测子集，且，则可测。
若，，则。
若，均为可测集，那么。

引理1 是上的可测函数，那么定义在上可测。

引理2 是上的非负函数，且令，则：

在上可测当且仅当在上可测。
若在上可测，则：

定理是上的可测函数，则在上可测。

有界变差函数

单调有界函数、处处可微且导数有界的函数均为有界变差函数。
上的实值函数是有界变差的当且仅当是两个有界的递增函数之差。
若函数在上是有界变差的，则几乎处处可微。

引理若递增且连续，则几乎处处存在，进而可测、非负，且。

李特尔伍德三大原理

第三原理：每个收敛序列接近于一直收敛序列。

定理（） 是定义在有限测度集合上的可测函数序列并且在上几乎处处收敛于。给定，能找到对应的闭集，使得且在上一致收敛于。

第二原理：每个可测函数接近于连续函数。

定理（） 在有限测度集合上可测且取有限值。给定，能找到对应的闭集，使得且在上连续。

绝对连续函数

定义对于定义在上的实值函数，若对任意，存在使得只要且区间内部不交就有

则称绝对连续(AC)。绝对连续函数具有以下性质：

AC函数是一致连续且有界变差的；
若可积，，则绝对连续，这是积分的绝对连续性保证的。
如果，那么对于任意中的零测集，；
如果，为中的可测集，那么可测；
若满足以下条件，。
- 如果，则；
- ；
- ，

绝对连续函数有着强于有界变差函数的结论：

定理如果，则几乎处处存在。此外，若几乎处处为零，则为常数。

投稿专区

2023年05月30日 19 字大概 1 分钟

1

新概念cp谁懂啊谁懂啊
Kreisler x Rachmaninov
磕

2023.5.30 from Nash

网易云音乐评论数据分析

2023年05月14日 4 字大概 1 分钟

点击这里

短地址生成器

2023年05月07日 1k 字大概 4 分钟

shorturl_generator短地址生成器

1.功能说明

这个小网站的功能便是把很长的地址转化为一个短地址，起到方便转发的作用。

所用到的技术栈：Python+Flask+html+MySQL。

实例：输入一长串地址如下

点击生成，得到的输出如下：

点击短链接立刻成功转到长链接对应的页面。

2.实验说明

2.1.概览

这个作业是一个典型的Flask框架，我也采用的是经典的布局：

app.py是主程序，里面是获取长链接页面和生成短链接页面的相关代码，通过GET和POST的方法实现前后端的联系；
config.py是Flask项目的配置文件，主要是数据库的连接信息；
models.py是自己撰写的类，里面设计了url在数据库中的表单形式，此外还设计了两个获取数据的方法；
exts.py专门用来存放SQLAlchemy的实例，这样做的原因见下文。
index.html是基于bootstrap的app页面，简洁美观。

大致的思路便是通过将网页的序号（在数据库里的序号）通过62进制函数形成一一对应并且缩短长度，再在本网页设置重定向即可。运作流程可以概括为：用户输入长链接->数据库存储长链接并且生成序号->(点击短链接时)通过短链接后缀找到序号，找到数据库中对应的长链接->跳转。

2.2作业中设计的类

models.py

from exts import db
class URLModel(db.Model):
    #数据表信息设置
    __tablename__ = "urls"
    id = db.Column(db.Integer, nullable=False, autoincrement=True, primary_key=True)
    url = db.Column(db.String(1000), nullable=False)
    #通过id找到对应url
    def find_url(self, id):
        url = URLModel.query.filter(URLModel.id == id).first().url
        return url
    #获取当前最后一个数据（即刚刚存储的数据）的id
    def find_id(self):
        return URLModel.query.order_by(URLModel.id.desc()).first().id

这个类先设计了url在数据库中的表单形式：id是url对应的序号，为整型变量，是整个table的主键并且有自增；url为字符串变量，存放用户输入的长url。Flask-SQLAlchemy提供一个名为 Model 的类，用于作为声明模型时的 declarative 基类。在这之后我设计了两个简单的方法，分别用数据库的语句查询到相应的信息，从而简化了主程序的代码。find_url通过输入id返回对应的url，find_id的作用是查询数据表最后一行对应的id。这个类的设计至关重要，因为主程序绝大多数功能都要调用这个类。

2.3实验中的问题及难点

（这个问题到现在还没解决）Python的虚拟环境问题。这个app分别在pycharm terminal跑和在进入虚拟环境的cmd上跑，用的包位置不一样。后面就统一在terminal里面跑得了。
（最坑爹的bug）

The current Flask app is not registered with this 'SQLAlchemy' instance.

为了解决这个报错，我先改变了代码的结构，新增了exts.py专门用来存放SQLAlchemy的实例，这样比较符合Flask的文件规范，也可以有效防止同时构建多个实例导致报错。然而报错仍然存在。搞了好几个小时才发现app.py中的初始化语句app = Flask(__name__)写了两遍！系统会觉得我创建了重复的实例就报错了。
（各种小bug）
- 下包失败，原因是我一开始挂了梯子，得关掉。
- 要下载的库是bases.py而我一开始下载的是bases。正确的语句是pip3 install bases.py。
- 数据库连不上，后面修改了配置文件就成功了。
- 设计的函数返回值的类型错误，这是小失误，很快解决。
（难点）其实每个模块单独来看真的不难，对我来说最难的部分就是这个项目技术栈之间的联系，比如说Flask和MySQL的联系；app与网页的联系；表单和数据库的联系等等。这往往是最容易出bug的地方。