[置顶]站点公告
本博客现在在主页展示的主要是学习相关内容,吹水的,或者一些日寄之类的琐碎文章放在了本站隐藏专栏里面。
(2023/4/30)
长时间停更了,身上的事情有些琐碎。以后有望在这里开设泛函分析的专栏。哈哈,加油!
(2023/9/20)
恢复更新!
(2023/11)

本博客现在在主页展示的主要是学习相关内容,吹水的,或者一些日寄之类的琐碎文章放在了本站隐藏专栏里面。
(2023/4/30)
长时间停更了,身上的事情有些琐碎。以后有望在这里开设泛函分析的专栏。哈哈,加油!
(2023/9/20)
恢复更新!
(2023/11)


占坑,泛函分析复习笔记,内容大概有:
到2.2章节除了1.5章所有作业题解答以及部分未布置的题;
部分定理手动证明;
往届期中真题自己的解答;(不正式写了)
向量族的元线性无关,即对于任意有限子集
对于任何
注意:任意向量空间均存在
强调(1.3里面常用结论)
中任意有界集为列紧集;
- 列紧空间的任意(闭)子集都是(自)列紧集;
- 列紧空间必是完备空间;
- 完全有界的度量空间可分。
定理 任何有限维
要证明这个定理,首先有:有限维
设
则有
定理 设
证明 由稠密性,设
首先可以假设对任何
那么,
定理 任意向量空间均可赋范。
证明 取
此即
定理 赋范空间
定理
证明 不妨证
$$
A:=\bigcup\limits_{n=1}^\infty{(y_i){i=1}^\infty\in\mathcal{l}^p;y_i\in\mathbb{Q}\ when \ i\leq n,y_i=0\ elsewhere}.
$$
定理
强调(有限维的情况)
- 任意两个范数等价;
- 任何有限维赋范空间可分;
- 对于有限维赋范空间中的子集,紧等价于有界闭;
空间 的有限维子空间在 中闭;
空间 是有限维的等价于 的单位球面列紧。
证明第三条:对于
,由于紧蕴含有界闭只需反过来证明 自列紧。取 的 基 ,有界推得各个系数有界,故找到了收敛的子列,这证明了自列紧。
定理
证明 取
这时取一个
定理
证明 选取基展开,证明
定理(投影映射相关)
定理(正交补相关)
如果
定理(
例子(
在希尔伯特空间
以序列空间
尽管
因此,
未完待续…
设定义在
上的函数 满足 。若 且 ,证明 。
不妨设
对于有界零测集
设
是 上的连续函数, 是 上的实值可测函数,则 是 上的可测函数。
上可测函数列 满足 ,且 依测度收敛到0,证明 。
是 上的正值可积函数, 是一列可测子集,且有 ,证明 。
设存在一列
这推出
补充上面的定理证明:
对于给定的度量空间
证明:所有的
总的来说,就是Fatou引理加上
考试可能涉及到各种收敛性,这里做出一定总结:
引理1 若
证明:
Egorov定理
证明我看过一遍了,要用到上面的引理。取定
从而构造
进一步说明
注意
定理
由上述引理1立即得证。
Riesz定理 依测度收敛序列存在几乎处处收敛子列。
Lusin定理描述了可测函数和连续函数的关系。其叙述如下:
首先我们需要知道,对于可测函数
推论1
若
推论2
设
,证明 。
证明:等价于证明级数
第一步是因为
对
证明思路:先证明对简单函数成立,再用简单函数逼近可测函数。
首先,DCT证明了更强的
推论1(逐项积分)
不同于非负可测函数列的逐项积分定理,这里的表述是:
设
证明:
从而
推论2(积分号下求导)
那么有如下成立:
证明:当
再利用DCT,得到:
平均连续性:
Fubini定理和Tonelli定理部分在周民强上已经过了一遍了,就不在这里写了
引理2 设
证明思路:表达式写开,用Tonelli定理再加上平均连续性即得。
Lebesgue微分定理(一维版本) 设
证明:
step1,
step2,因为
step3,证明
定理对于
推论 若
证明:将Lebesgue微分定理应用于函数
记
, ,则 ,且 。
定义 对于定义在
则称
AC函数是一致连续且有界变差的;
如果
微积分基本定理成立;
如果
如果
若
如果
绝对连续函数有着强于有界变差函数的结论:
定理 如果
暂时更新到这里,剩下的时间要回顾stein上的习题,再就泡在周民强里面了。晚上争取把chap2的习题全都过一遍。
考虑下面的问题:
给定区间
上的一个具有正测度的类 集合 , 的补集记为 。对于 上的特征函数 ,考虑 在 上点处的导数,这是否 为0?
这一点由于
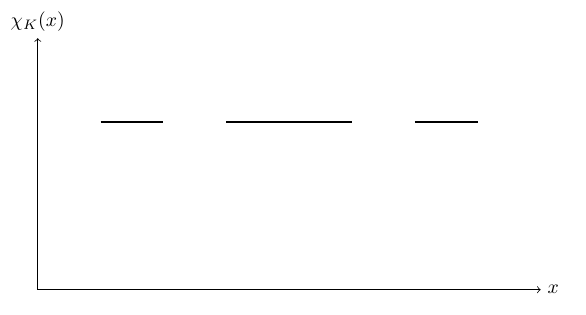
选定一个
引理 对于支撑在有限测度集合
这样,定义BF函数
而对于非负函数
对于一般的函数
定理(有界收敛定理)
总结来说就是有界BF函数+几乎处处收敛推得可积+积分值收敛。
定理(法图引理)
这是一个很反直觉的结果,这个结论的证明也相当巧妙。简言之就是选取了
推论
相应地单调收敛定理是更弱的推论。一个有用的推论是,无穷非负可测函数项级数的积分可以逐项积分。
可积函数的重要性质
第一个结论,令
控制收敛定理
为了证明勒贝格微分定理,我们先引入哈代-李特尔伍德极大函数。
定义(哈代-李特尔伍德极大函数) 对于
极大函数具有以下性质:
(弱型不等式)对所有
此外还有性质如:
对
若对于
(3)的形式比切比雪夫不等式弱。切比雪夫不等式说的是,对于非负可测函数
这个不等式放缩其实很松。将
定理的证明是构造性的。我们先选出最大的球
(3)的证明:
要证明
取定
命题得到了证明。下面着手证明勒贝格微分定理。
仅需证明对每个
测度为0。由于紧支撑连续函数在
两边同时取上极限并且利用三角不等式得到:
再定义:
则由切比雪夫不等式和弱型估计得到:
显然有包含关系
remark:对于局部可积函数,上述结论仍然成立。
其他定义及结论:
定义(勒贝格密度点)
则几乎每个
定义(勒贝格集)
的
定理 向量空间
推论
定理 以下函数簇在
简单函数(有限测度可测集的特征函数的有限线性组合)
阶梯函数(cube的特征函数的有限线性组合)
紧支撑连续函数
平移不变性
这是紧支撑连续函数在
假定
此外,还满足等式:
作为一个应用,有如下的结论:
推论 对
引理1
引理2
若
定理
单调有界函数、处处可微且导数有界的函数均为有界变差函数。
若函数
引理 若
第三原理:每个收敛序列接近于一直收敛序列。
定理(
第二原理:每个可测函数接近于连续函数。
定理(
定义 对于定义在
则称
AC函数是一致连续且有界变差的;
若
如果
如果
若
如果
绝对连续函数有着强于有界变差函数的结论:
定理 如果
新概念cp谁懂啊谁懂啊
Kreisler x Rachmaninov
磕
这个小网站的功能便是把很长的地址转化为一个短地址,起到方便转发的作用。
所用到的技术栈:Python+Flask+html+MySQL。
实例:输入一长串地址如下

点击生成,得到的输出如下:
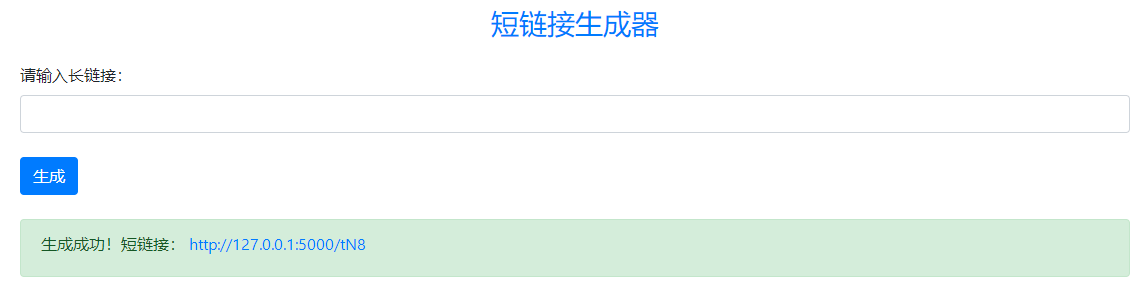
点击短链接立刻成功转到长链接对应的页面。
这个作业是一个典型的Flask框架,我也采用的是经典的布局:
app.py是主程序,里面是获取长链接页面和生成短链接页面的相关代码,通过GET和POST的方法实现前后端的联系;
config.py是Flask项目的配置文件,主要是数据库的连接信息;
models.py是自己撰写的类,里面设计了url在数据库中的表单形式,此外还设计了两个获取数据的方法;
exts.py专门用来存放SQLAlchemy的实例,这样做的原因见下文。
index.html是基于bootstrap的app页面,简洁美观。
大致的思路便是通过将网页的序号(在数据库里的序号)通过62进制函数形成一一对应并且缩短长度,再在本网页设置重定向即可。运作流程可以概括为:用户输入长链接->数据库存储长链接并且生成序号->(点击短链接时)通过短链接后缀找到序号,找到数据库中对应的长链接->跳转。
models.py
1 | from exts import db |
这个类先设计了url在数据库中的表单形式:id是url对应的序号,为整型变量,是整个table的主键并且有自增;url为字符串变量,存放用户输入的长url。Flask-SQLAlchemy提供一个名为 Model 的类,用于作为声明模型时的 declarative 基类。在这之后我设计了两个简单的方法,分别用数据库的语句查询到相应的信息,从而简化了主程序的代码。find_url通过输入id返回对应的url,find_id的作用是查询数据表最后一行对应的id。这个类的设计至关重要,因为主程序绝大多数功能都要调用这个类。
(这个问题到现在还没解决)Python的虚拟环境问题。这个app分别在pycharm terminal跑和在进入虚拟环境的cmd上跑,用的包位置不一样。后面就统一在terminal里面跑得了。
(最坑爹的bug)
The current Flask app is not registered with this 'SQLAlchemy' instance.
为了解决这个报错,我先改变了代码的结构,新增了exts.py专门用来存放SQLAlchemy的实例,这样比较符合Flask的文件规范,也可以有效防止同时构建多个实例导致报错。然而报错仍然存在。搞了好几个小时才发现app.py中的初始化语句app = Flask(__name__)写了两遍!系统会觉得我创建了重复的实例就报错了。
(各种小bug)
下包失败,原因是我一开始挂了梯子,得关掉。
要下载的库是bases.py而我一开始下载的是bases。正确的语句是pip3 install bases.py。
数据库连不上,后面修改了配置文件就成功了。
设计的函数返回值的类型错误,这是小失误,很快解决。
(难点)其实每个模块单独来看真的不难,对我来说最难的部分就是这个项目技术栈之间的联系,比如说Flask和MySQL的联系;app与网页的联系;表单和数据库的联系等等。这往往是最容易出bug的地方。
内积空间:
赋范空间:
定义内积诱导的范数
定义范数诱导的度量
完备度量空间:每个柯西列都收敛.
连续函数的
矩阵范数:对于
命题:
常见的完备度量空间:
注意:有限维赋范线性空间都是完备的,赋范线性空间里,完备等价于闭。
紧致:度量空间
结论:
定义(连续函数) 以下是
压缩映射:
若
定义(一致连续)
定义(连通):度量空间
定义(弧连通):度量空间
定理:




